Abstract
The Core Idea: Minimal-Sufficient Concepts
We propose applying the Information Bottleneck (IB) principle directly to the concept layer. The goal is to create a “minimal-sufficient” representation.
In technical terms, the model is trained to minimize the mutual information between the raw input $X$ and the concepts $C$ (denoted as $I(X;C)$), while simultaneously maximizing the mutual information between the concepts $C$ and the target labels $Y$ (denoted as $I(C;Y)$). This creates a “squeeze”: the model must retain enough information to predict the target label accurately, while it is forced to discard spurious details from the input image that do not contribute to the specific concepts.
We derived two practical training objectives to implement this framework: a variational objective ($\text{IB}_B$) and an estimator-based CIB ($\text{IB}_E$) that uses an entropy-based surrogate that performs on par with the variational bound.

Our proposed CIBMs pipeline. The image is encoded through $p(z \mid x)$, which in turn encodes the concepts with $q(c \mid z)$, and the labels are predicted through $q(y \mid c)$. These modules are implemented as neural networks. We introduced the IB regularization as mutual information optimizations over the variables as shown in dashed lines.
Restuls
Higher Accuracy: Evaluated across six CBM families and three datasets (CUB, AwA2, and aPY), CIBMs consistently outperformed their unregularized counterparts. On the aPY dataset, the regularizers even allowed the interpretable models to surpass the accuracy of the “black-box” baseline.
Reduced Concept Leakage: The models achieved significantly lower concept leakage, as measured by Oracle and Niche Impurity Scores (OIS and NIS), proving that they successfully filter out irrelevant input information.
More Reliable Interventions: In test-time intervention experiments, CIBMs demonstrated a smooth, monotonic increase in accuracy as concepts were corrected. This contrasts with baseline models (like soft-joint CBMs), which often exhibited performance dips or instability when users intervened on concepts.
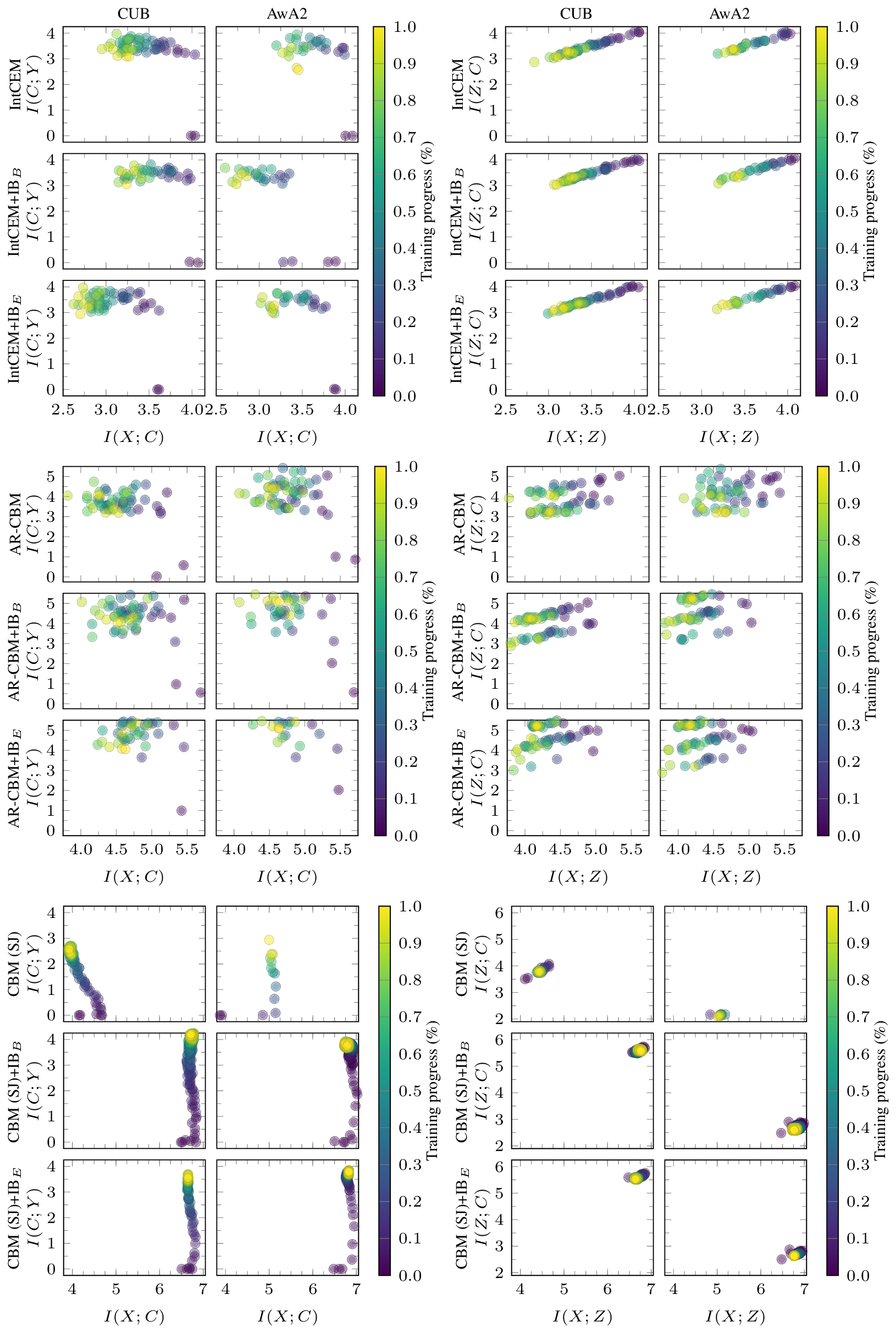
Information plane dynamics (in nats) for (top) IntCEM, (middle) AR-CBM, (bottom) CBM (SJ) and our proposed methods, $\text{IB}_B$ and $\text{IB}_E$ . Warmer colors denote later steps in training. We show the information plane between the variables X, C, and Y ; and the variables X, Z, and C.
Citation
@inproceedings{galliamov2026,
title={Concepts' Information Bottleneck Models},
author={Galliamov, Karim and Kazmi, Syed M Ahsan and Khan, Adil and Ram\'irez Rivera, Ad\'in},
booktitle={The Fourteenth International Conference on Learning Representations},
year={2026},
url={https://openreview.net/forum?id=JGIYfwaNpT}
}