Abstract
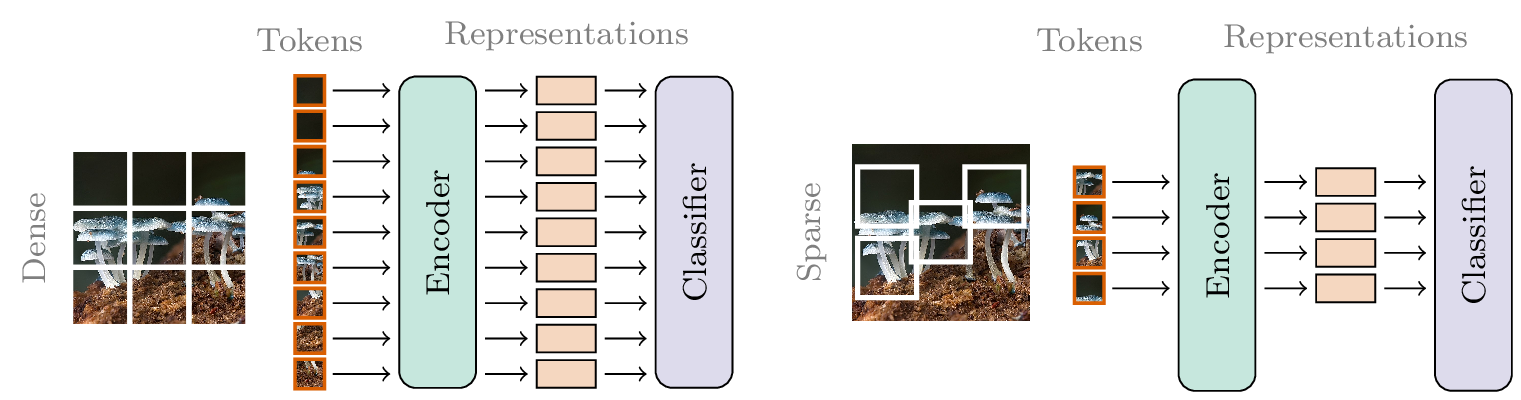 Figure 1: (Left) Astandard ViT splits the image into a fixed grid of non-overlapping patches. (Right) With SPoT, an adaptively chosen subset of subpixel-precise patches are extracted.
Figure 1: (Left) Astandard ViT splits the image into a fixed grid of non-overlapping patches. (Right) With SPoT, an adaptively chosen subset of subpixel-precise patches are extracted.
Sparsity - the fine art of doing more with less - is an attractive prospect in systems design and modeling. As models grow ever larger, sparse features alleviates the computational demands of a model to provide lower latency, lower memory overhead, and higher throughput - all indispensable properties for real-time applications. Incidentally, sparse selection of features offers inherent interpretability and transparency for increasingly complex models
Vision Transformers (ViTs) can naturally be adapted to sparse inputs via their Bag-of-Visual-Words (BoVW) representation of images as a collection of patch tokens. However, in carefully studying the fine print of Dosovitskiy et al’s. work, one notes an insistence on aligning features with an underlying grid, mirroring the structure inherited by its language counterpart where inputs are naturally represented as sequences of discrete tokens. Our work posits that this adherence turns sparsity into an awkward dance; forcing the selection of entire tiles, even if the true optimal feature set hides in-between rigid lines. Like eating soup with a fork: possible, but decidedly inefficient and frustrating.
We propose a simple remedy via Subpixel Placement of Tokens (SPoT). By allowing patches to occupy continuous subpixel positions instead of constraining features to a discrete grid, we expand our modeling toolbox to include gradient based search and sampling for discovering optimal sparse feature sets.
Problem Statement: Sparse Feature Selection in ViTs
We denote a ViT encoder as $g_\theta : \mathcal{I} \times \Omega \to \mathbb{R}^d$, where $\mathcal{I}$ is a dataset of source images, and $\Omega$ is a space of positions from which to sample image features. With standard tokenization $\Omega_\text{grid}$ is a fixed, discrete set of non-overlapping square patches tiling the image with a fixed window size on a grid of pixels. The sparse feature selection (SFS) problem can then be formulated as
\[\begin{align} \min_\phi \mathbb{E}_{S \sim p_\phi} \big[\mathcal{L}(g_\theta(I,S), y) \big] \ \text{s.t.}\ S \subseteq \Omega, \,\,\, |S| \ll |\Omega|. \end{align}\]In other words, we are looking for a probability distribution $p_\phi$ over subsets of $\Omega$ that minimizes a loss function $\mathcal{L}$. We note that for the discrete non-overlapping case of $\Omega_\text{grid}$, there is an implicit assumption that sampling of $S$ is done without replacement, since sampling the same feature more than once is unlikely to improve model performance. Three specific issues arise from the ViT sparse sampling problem;
- Interdependence: Transformers process tokens as a set. This means that the marginal distribution of one token is dependent on the inclusion of other tokens. Furthermore, the optimal distribution $p_\phi$ for a given image may vary depending on the choice of number of tokens.
- Combinatorial search: The discrete nature of $\Omega_\text{grid}$ means that selecting a subset of tokens is combinatorial knapsack problem. This makes search difficult and gradient methods intractable, particularly since cardinality-constrained subset selection is NP-hard.
- Misalignment: By quantizing patches to a fixed grid, key patterns for discriminating an image could be missed in SFS. Concretely, if the grid imposed by $\Omega_\text{grid}$ is misaligned with key features in the image, SFS could be challenging, as a central shape or texture may be spread over multiple patches, making subset selection more challenging.
These issues hinder efficient optimization of SFS under standard tokenization - in other words, we posit that grids cannot align every salient region.
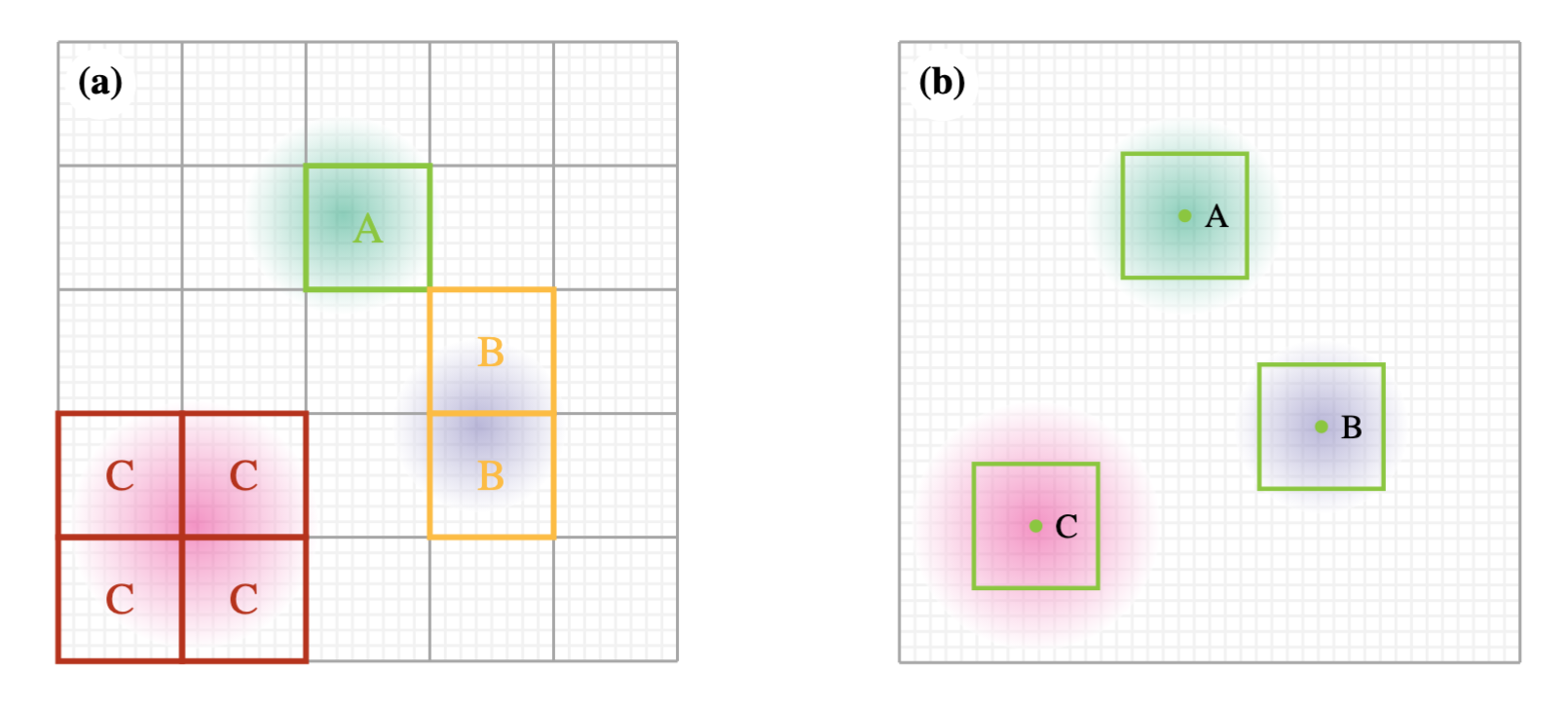 Figure 2: A $5 \times 5$ patch grid (gray) with three optimal region placements for sparse feature selection. (a) The green patch is well aligned (A), yellow straddles two cells (B), and red lies on a corner (C) and leaks into four cells. Translating the grid only swaps which peak is misaligned—one patch is always bad. (b) Our subpixel tokenizer drops fixed-size windows (\textcolor{ok}{green} squares) directly on each peak, eliminating the alignment trade-off while still allowing conventional grid tokens when they \emph{are} well aligned.
Figure 2: A $5 \times 5$ patch grid (gray) with three optimal region placements for sparse feature selection. (a) The green patch is well aligned (A), yellow straddles two cells (B), and red lies on a corner (C) and leaks into four cells. Translating the grid only swaps which peak is misaligned—one patch is always bad. (b) Our subpixel tokenizer drops fixed-size windows (\textcolor{ok}{green} squares) directly on each peak, eliminating the alignment trade-off while still allowing conventional grid tokens when they \emph{are} well aligned.
Methodology: SPoT in a Nutshell
We propose a more flexible tokenization scheme to tackle SFS problems in ViTs. Instead of considering $\Omega$ as a fixed discrete partition, we instead imagine ${\Omega_\text{subpix} = [0,H-1] \times [0,W-1]}$ as a continuous space of subpixel positions from which to select features within a $H \times W$ image. We parametrize a subset of positions $S = { s_1, \dots, s_m }$ as a set of points of interest from which to extract features from within an image. By sampling tokens from continuous subpixel positions, our tokenizer directly addresses the intrinsic misalignment issue imposed by traditional grid‐based methods, as illustrated in \Cref{fig:sfs-misalignment}. To tackle the combinatorial search problem, we use a bilinear interpolation function $q$ and window size $k$, each subpixel position $s_i = (h,w)$ provides an extracted feature
\[\begin{align} I_q(s_i ; k) &= I_q(h-\tfrac{k}{2}\!:\!h+\tfrac{k}{2}, \; w-\tfrac{k}{2}\!:\!w+\tfrac{k}{2}). \end{align}\]This allows us to formulate SFS as a continuous, probabilistic optimization problem rather than an intractable discrete subset‐selection. The key insight is that our novel tokenizer allows us to (1) investigate placing different priors on $p_\phi$, and (2) use gradient based optimization to search for $S$ by way of gradients through $I_q$. Since we select $q$ to be bilinear, its partial derivatives w.r.t. $s$ exist everywhere except at pixel boundaries, so gradients propagate cleanly back to the placements ${s_1,\dots,s_m}$. Note that subpixel tokens do not impose any constraint on non-overlapping patches.
Since ${\Omega_\text{grid} \subseteq \Omega_\text{subpix}}$, patch tokenization is just a special case of our tokenization method. This means that models can be evaluated with the exact same features as a standard patch-based ViT by letting $S = \Omega_\text{grid}$.
Spatial Priors
By removing the strict adherence to grids in ViTs, we can leverage more continuous spatial priors for token placements for optimal feature extraction. We compare several spatial priors, each encoding different assumptions about feature importance and spatial distribution.
- Uniform: randomly samples locations with no spatial bias, assuming all regions are equally important.
- Gaussian: randomly samples locations with a central bias, which encodes a prior belief that subjects are typically centered in images.
- Sobol: provides quasirandom sampling aimed at uniform coverage while reducing overlap.
- Isotropic: deterministically distributes tokens evenly in a subpixel grid, emphasizing coverage.
- Center: deterministically distributes tokens evenly with slight central-bias.
- Salient: encodes object-centric bias by placing tokens based on regions identified as visually salient from a pretrained saliency model.
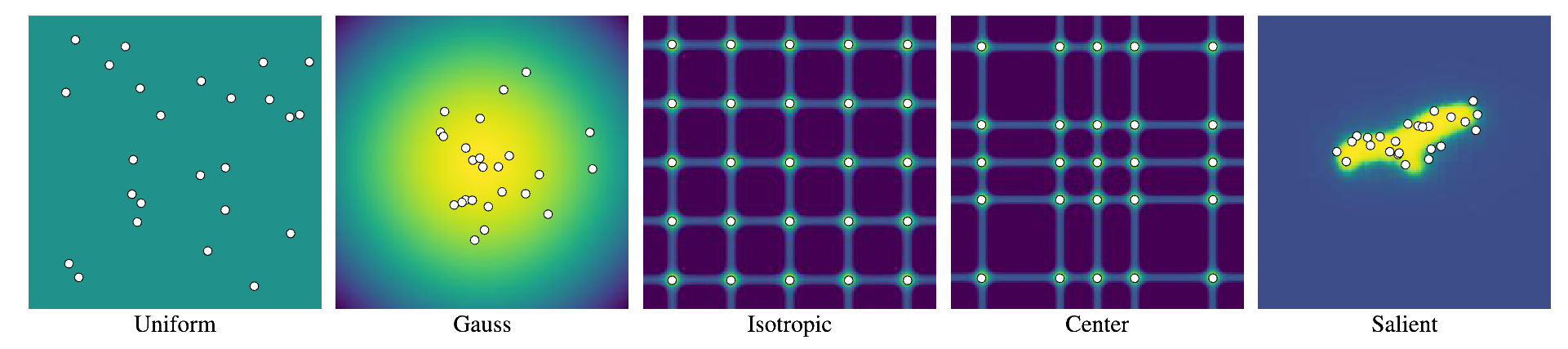 Figure 3: An illustration of different spatial priors investigated with SPoT.
Figure 3: An illustration of different spatial priors investigated with SPoT.
Exploring Oracle Neighbourhoods with SPoT-ON
In addition to investigating spatial different spatial priors, we also look to directly explore differentiable optimization for token placement. To probe for ideal choices of $S = {s_1, \dots, s_m }$, we optimize a constrained version of the SFS problem directly for each image. We freeze the encoder $g_\theta$, and optimize
\[\begin{align} \underset{S}{\arg\min} \; \big[ \mathcal{L}(g_\theta(I,S), y) \big] \ \text{s.t.}\ S \subseteq \Omega_\text{subpix}, \ |S| = m \end{align}\]for a set number of tokens $m$ with initial positions ${S^0 \sim p_\phi}$ sampled from a chosen prior $p_\phi$.
Gradient optimization provides an Oracle Neighborhood guided (ON) adjustments of the initial placements with SPoT.
SPoT-ON reveals locations are optimal for classifying each image, which allows us to ascertain the existence of an optimal set of positions $S$ for each image, and estimate an upper bound on performance gain from effective token sampling.
 Figure 4: Illustration of oracle placements with 25 tokens with SPoT-ON. By optimizing our oracle-neighborhood search through the model, the oracle discovers optimal placement of points, yielding an accuracy of $90.9\%$ on ImageNet1k with only $\sim12.5\%$ of the tokens. Trajectories are colored with dark purple for initial points, and endpoints colored bright yellow.
Figure 4: Illustration of oracle placements with 25 tokens with SPoT-ON. By optimizing our oracle-neighborhood search through the model, the oracle discovers optimal placement of points, yielding an accuracy of $90.9\%$ on ImageNet1k with only $\sim12.5\%$ of the tokens. Trajectories are colored with dark purple for initial points, and endpoints colored bright yellow.
Experiments and Key Findings
We design four case studies for SPoT to determine the effectiveness and properties of subpixel tokenization in sparse regimes.
- Are Grids an Inherent Limitation of ViTs? Off-grid token placement enables greater flexibility and yields substantially better performance than grid-based approaches under sparse token settings.
- Do Object-Centric Priors Improve Predictions? Object-centric priors yield higher performance in sparse regimes. In dense regimes, even and structured coverage provides better performance.
- Does Oracle Guidance Prefer Salient Regions? While oracle gradient search yields a slight bias toward higher-saliency pixels, the results are not conclusive. Assessments of token trajectories suggest that token interdependency, rather than saliency alone, predominantly determines final placements.
- Do Oracle Guided Placements Transfer? Discovered positions generalize between models; a set of placements optimized via a model will improve results with another independently trained model.
Full Experimental Results
We report classification top-1 and kNN accuracies for supervised and and self-supervised models using different token priors. Our results show that center-bias in spatial priors is beneficial in sparse regimes, while coverage becomes more important as token budgets increase.
Backbone: CLS-IN21k
| Model | Prior | Oracle | 25 T Acc\@1 | 25 T kNN | 49 T Acc\@1 | 49 T kNN | 100 T Acc\@1 | 100 T kNN | 196 T Acc\@1 | 196 T kNN |
|---|---|---|---|---|---|---|---|---|---|---|
| ViT-B/16 | Patch Grid | 24.72 | 27.86 | 56.29 | 57.19 | 78.75 | 78.77 | 85.11 | 83.96 | |
| SPoT-B/16 | Uniform | 44.05 | 45.23 | 67.77 | 66.38 | 79.64 | 78.03 | 83.76 | 81.85 | |
| SPoT-B/16 | Gaussian | 45.22 | 45.27 | 68.64 | 66.96 | 79.75 | 77.74 | 83.45 | 81.48 | |
| SPoT-B/16 | Sobol | 43.67 | 46.48 | 69.02 | 68.60 | 81.63 | 79.35 | 84.66 | 82.62 | |
| SPoT-B/16 | Isotropic | 46.85 | 48.19 | 70.61 | 70.29 | 82.20 | 80.73 | 85.15 | 83.42 | |
| SPoT-B/16 | Center | 52.45 | 52.18 | 69.22 | 68.16 | 80.84 | 78.56 | 84.01 | 82.23 | |
| SPoT-B/16 | Salient | ✓ | 55.71 | 56.65 | 72.89 | 72.38 | 79.91 | 80.56 | 84.56 | 82.59 |
| SPoT-ON-B/16 | Isotropic | ✓ | 81.70 | 70.65 | 94.28 | 88.58 | 95.97 | 92.92 | 96.12 | 93.52 |
Backbone: CLS-IN1k
| Model | Prior | Oracle | 25 T Acc\@1 | 25 T kNN | 49 T Acc\@1 | 49 T kNN | 100 T Acc\@1 | 100 T kNN | 196 T Acc\@1 | 196 T kNN |
|---|---|---|---|---|---|---|---|---|---|---|
| ViT-B/16 | Patch Grid | 9.24 | 12.05 | 41.05 | 44.38 | 71.22 | 71.41 | 79.14 | 77.64 | |
| SPoT-B/16 | Uniform | 29.87 | 33.88 | 60.64 | 60.84 | 74.44 | 73.18 | 79.38 | 77.36 | |
| SPoT-B/16 | Gaussian | 29.27 | 33.07 | 60.47 | 60.23 | 74.37 | 72.82 | 79.02 | 77.00 | |
| SPoT-B/16 | Sobol | 30.67 | 35.23 | 64.42 | 63.88 | 76.45 | 75.18 | 79.96 | 78.17 | |
| SPoT-B/16 | Isotropic | 33.52 | 37.84 | 66.18 | 66.25 | 77.58 | 76.29 | 80.61 | 79.04 | |
| SPoT-B/16 | Center | 39.91 | 42.47 | 63.04 | 62.65 | 75.41 | 73.63 | 79.32 | 77.71 | |
| SPoT-B/16 | Salient | ✓ | 39.83 | 43.72 | 66.32 | 66.00 | 74.36 | 75.25 | 79.54 | 78.03 |
| SPoT-ON-B/16 | Isotropic | ✓ | 73.99 | 74.42 | 94.21 | 90.11 | 95.79 | 93.61 | 96.04 | 93.97 |
Backbone: MAE-IN1k
| Model | Prior | Oracle | 25 T Acc\@1 | 25 T kNN | 49 T Acc\@1 | 49 T kNN | 100 T Acc\@1 | 100 T kNN | 196 T Acc\@1 | 196 T kNN |
|---|---|---|---|---|---|---|---|---|---|---|
| ViT-B/16 | Patch Grid | 55.43 | 48.85 | 70.69 | 67.15 | 79.53 | 78.41 | 83.60 | 82.07 | |
| SPoT-B/16 | Uniform | 56.71 | 49.72 | 73.22 | 65.85 | 80.53 | 74.76 | 82.78 | 78.21 | |
| SPoT-B/16 | Gaussian | 57.58 | 49.49 | 72.51 | 65.59 | 80.31 | 74.52 | 82.55 | 77.90 | |
| SPoT-B/16 | Sobol | 60.62 | 53.54 | 75.71 | 68.71 | 82.19 | 76.24 | 83.51 | 79.09 | |
| SPoT-B/16 | Isotropic | 61.72 | 54.56 | 76.84 | 70.02 | 82.76 | 77.24 | 83.89 | 79.53 | |
| SPoT-B/16 | Center | 62.83 | 55.61 | 74.63 | 67.31 | 81.06 | 75.20 | 82.97 | 78.54 | |
| SPoT-B/16 | Salient | ✓ | 66.13 | 60.80 | 77.10 | 72.24 | 81.46 | 77.25 | 81.64 | 79.13 |
| SPoT-ON-B/16 | Isotropic | ✓ | 90.93 | 79.73 | 94.87 | 87.87 | 96.09 | 90.76 | 96.24 | 91.28 |
Performance Gap
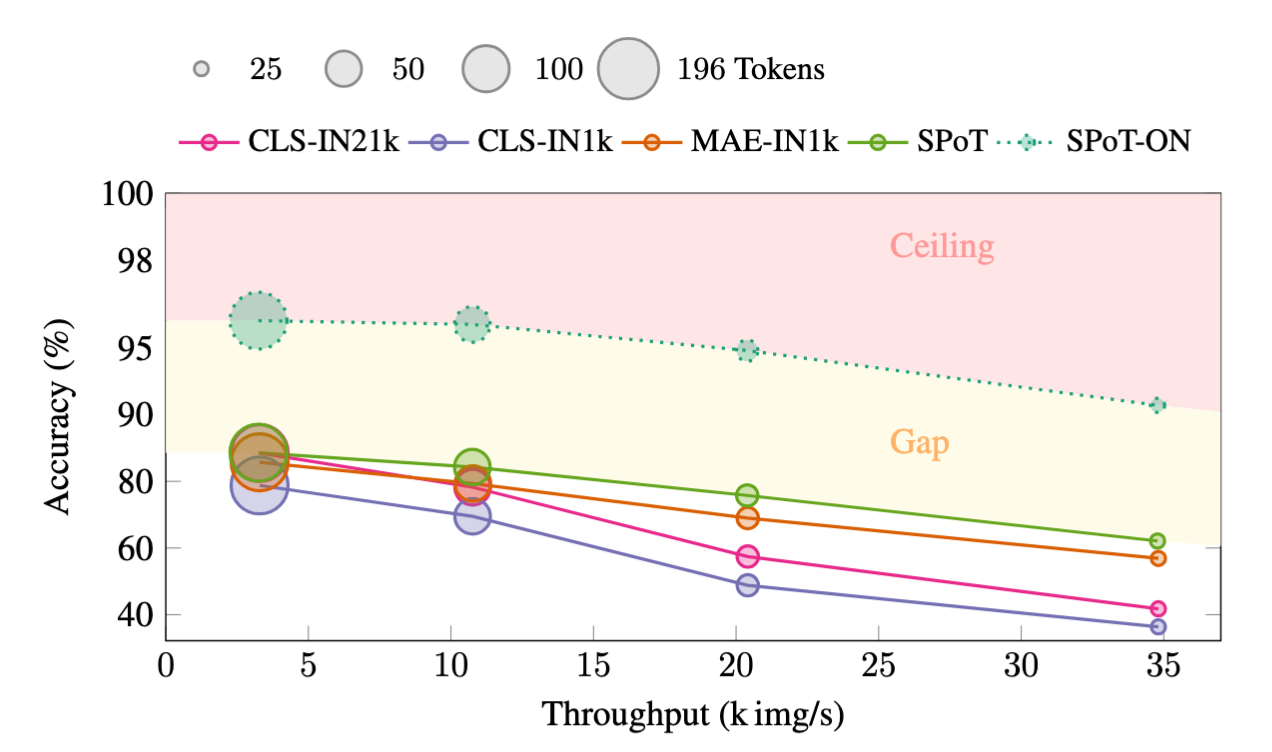 Figure 5: We show ImageNet1k accuracy vs throughput with 5 models at four sparsity levels. The ceiling area denotes performance unlikely to be achieved given the intrinsic label noise in ImageNet. The gap highlights the margin between SPoT with optimal configuration and SPoT-ON, illustrating possible performance gain through better token placement.
Figure 5: We show ImageNet1k accuracy vs throughput with 5 models at four sparsity levels. The ceiling area denotes performance unlikely to be achieved given the intrinsic label noise in ImageNet. The gap highlights the margin between SPoT with optimal configuration and SPoT-ON, illustrating possible performance gain through better token placement.
Figure 5 shows image throughput versus accuracy, comparing SPoT with the baselines across varying sparsity levels. As sparsity increases, throughput improves significantly, albeit with an associated trade-off in accuracy. Notably, SPoT achieves the most favorable trade-off, maintaining substantially more of the full-model accuracy while enabling higher throughput than competing approaches. We observe only slight variation in throughput between the models at each sparsity level, indicating that SPoT incurs very minimal computational overhead compared to baselines. Our oracle-guided variant SPoT-ON is included in the figure, and illustrates a ceiling on achievable performance in sparse regimes when placements are ideally sampled.
Summary
SPoT is a novel flexible tokenization framework for Vision Transformers that naturally adapts to sparse feature selection, and provides inherent methods for discovering optimal subpixel placements for extracting optimal features for prediction tasks. Our work highlights a gap for achievable improvements on classification tasks, and shows that sparse token selection can be significantly improved via more flexible tokenization schemes.
Limitations
In this study, we focus on analyzing the effects of subpixel tokenization under varying sparsity configurations with different spatial priors, the development of learnable spatial priors is a next step towards narrowing the oracle performance gap. By enabling continuous token positioning, SPoT facilitates gradient-based optimization of token placement, which can be advantageous in resource-constrained environments where sparsification is beneficial. Although we limit our scope to employ an oracle to determine optimal token placements, exploring oracle-independent strategies represents a compelling direction for future research. Specifically, integrating efficient saliency-driven objectives or heuristics during inference could potentially enhance throughput efficiency while maintaining competitive performance compared to models utilizing a full token budget.
Citation
@inproceedings{hjelkremtan2025spot,
title={{SPoT}: Subpixel Placement of Tokens in Vision Transformers},
author={Hjelkrem-Tan, Martine and Aasan, Marius and Arteaga, Gabriel Y. and Ram\'irez Rivera, Ad\'in},
journal={{CVF/ICCV} Efficient Computing under Limited Resources: Visual Computing ({ECLR} {ICCVW})},
year={2025}
}